GAN 基本介绍
GAN的基本组成
生成器(Generator) G
- Generator是一个函数,输入是z, 输出是x
- 给定一个先验分布$P_{prior}(\bf z)$和一个生成器$G$决定的分布$P_G{(\bf x)}$
判别器(Discriminator) D
- Discriminator 是一个函数,输入是$\bf x$,输出是一个标量
- 函数的作用是评估$P_{G}(\bf x)$和$P_{data}(\bf x)$之间到底有多不同
函数(Function) V(G,D)
$$
V = E_{x\sim P_{data}}[\log {D(x)}] + E_{x\sim P_{G}}[\log {(1-D(x))}]
$$
D(x)可以简单理解为将x数据判别为真实数据的概率。这里函数V的作用是衡量$P_G(x)$和$P_{data}(x)$之间不同的程度。
GAN目标
判别器目标是为了尽可能区分真实数据和生成器生成的数据的区别。也就是尽可能使得$P_G(x)$和$P_{data}(x)$之间不同。
也就是
$$
D^* = \arg \max_D V(G,D)
$$生成器的目标是为了让自己生成的数据尽可能地不被判别器区分出和真实数据的不同,也就是使得判别器下判别$P_G(x)$和$P_{data}(x)$之间不同程度尽可能小
也就是
$$
G^* = \arg \min_G \max_D V(G,D)
$$结论:
$$
D^* = \arg \max_D V(G,D) = -\log 4 + 2 JSD(P_{data}(x) || P_G(x))
$$
引入KL散度,JS散度相对熵,又称KL散度,是描述两个概率分布P和Q差异的一种方法。它是非对称的,这意味着KL(P||Q) != KL(Q||P) 。特别的,在信息论中,KL(P||Q)表示当用概率分布Q来拟合真是分布P时,产生的信息损耗,其中P表示真是分布,Q表示P的拟合分布。
$$
KL(P||Q) = \sum_x P(x) \log \frac{P(x)}{Q(x)}
$$
相对熵可以衡量两个随机分布之间的距离当两个随机分布相同时,它们的相对熵为0,当两个随机分布的差别增大时,它们的相对熵也会增大。JS散度
$$
JSD(P||Q) = \frac{1}{2} KL(P||\frac{P+Q}{2}) + \frac{1}{2}KL(Q || \frac{P+Q}{2})
$$
Proof:
$$
\begin{aligned}
\max_D V(G,D)
& = V(G , D^) = E_{x\sim P_{data}}[\log D^(x)] + E_{x\sim P_G}[\log(1-D^*(x))] \\
& = E_{x\sim P_{data}}[\log \frac{P_{data}(x)}{P_{data}(x) + P_G(x)}] + E_{x\sim P_G}[\log \frac{P_{G}(x)}{P_{data}(x) + P_G(x)}] \\
& = \int_x P_{data}(x)\log \frac{P_{data}(x)}{P_{data}(x) + P_G(x)} d_x + \int_x P_{G}(x)\log \frac{P_{G}(x)}{P_{data}(x) + P_G(x)} d_x \\
& = \int_x P_{data}(x)\log \frac{\frac{1}{2}P_{data}(x)}{\frac{P_{data}(x) + P_G(x)}{2}} d_x + \int_x P_{G}(x)\log \frac{\frac{1}{2}P_{G}(x)}{\frac{P_{data}(x) + P_G(x)}{2}}d_x \\
& = \int_x P_{data}(x)\log \frac{1}{2} d_x + \int_x P_{data}(x)\log \frac{P_{data}(x)}{\frac{P_{data}(x) + P_G(x)}{2}} d_x \\
& + \int_x P_G(x)\log \frac{1}{2}d_x + \int_x P_{G}(x)\log \frac{P_{G}(x)}{\frac{P_{data}(x) + P_G(x)}{2}}d_x \\
& = 2 \log\frac{1}{2} + \int_x P_{data}(x)\log \frac{P_{data}(x)}{\frac{P_{data}(x) + P_G(x)}{2}} d_x + \int_x P_{G}(x)\log \frac{P_{G}(x)}{\frac{P_{data}(x) + P_G(x)}{2}}d_x \\
& = 2 \log\frac{1}{2} + KL(P_{data}(x) ||\frac{P_{data}(x) + P_G(x)}{2}) + KL(P_{G}(x) ||\frac{P_{data}(x) + P_G(x)}{2}) \\
& = -\log4 + 2JSD(P_{data}(x) || P_G(x))
\end{aligned}
$$
- 寻找最好的$G^$
$$
G^ = \arg \min_G \max_D V(G,D) = \arg \min_G -\log4 +2JSD(P_{data}(x) || P_G(x))
$$
那么使得最小化的G满足的条件是$P_{data}(x) = P_G(x)$
inclusion:
上述找到的$D^,G^$也满足了gan-net网络的最终目标,也就是最后判别器无法分清真实数据和生成数据,$P_{data}(x) = P_G(x)$。
算法结构
Semi Supervied GAN (SSGAN) 基于GAN的半监督学习
GAN的发明者Ian Goodfellow2016年在Open AI任职期间发表了这篇论文,其中提到了GAN用于半监督学习(semi supervised)的方法。称为SSGAN。
作者给出了Theano+Lasagne实现。本文结合源码对这种方法的推导和实现进行讲解。
核心理念
在半监督学习中运用GAN的逻辑如下。
无标记样本没有类别信息,无法训练分类器;
引入GAN后,其中生成器(Generator)可以从随机信号生成伪样本;
相比之下,原有的无标记样本拥有了人造类别:真。可以和伪样本一起训练分类器。
简单说明就是,给定的文本类别为k,将生成器(generator)生成的伪样本看作类别为k+1。那么最后输出的就是k+1维的softmax的向量,也就是对应每个类别的概率了。(ps: $softmax(x_i) = \frac{\exp(x_i)}{\sum_jexp(x_j)}$)
而最原始的Gan-net输出的实际上就只是一维的向量,因为它只需要一个数值来表示这个样本是真样本的概率。当这个概率为0.5时表示判别器无法判别生成器生成的数据了,从而达到了最好的效果。
原理
GAN中的两个核心模块是生成器(Generator)和鉴别器(Discriminator)。这里用分类器(Classifier)代替了鉴别器。
**真实类别数量为k,$x_f$表示生成的fake样本,将其标记为类别k+1,$x_l$表示真实的带标记数据,$x_u$表示真实的无标记数据, p是一个k+1维的概率向量**
三种误差
整个系统涉及三种误差。
对于训练集中的有标签样本,考察估计的标签是否正确。即,计算分类为相应的概率:
$$
L_{l}=−E[\ln p(y|x)]
$$
对于训练集中的无标签样本,考察是否估计为“真”。即,计算不估计为K+1K+1类的概率:
$$
L_u = -E[\ln \sum_{1<=i<=k} p(y_i | x)] = -E[\ln (1-p(k+1|x))]
$$
对于生成器产生的伪样本,考察是否估计为“伪”。即,计算估计为K+1K+1类的概率:
$$
L_f = -E[\ln p(k+1|x)]
$$
推导
考虑softmax函数的一个特性:
$$
\begin{aligned}
softmax(x_i−c)
& =\frac{exp(x_i−c)}{\sum_jexp(x_j−c)}=\frac{exp(x_i)/exp(c)}{\sum_jexp(x_j)/exp(c)} \\
& =\frac{exp(x_i)}{\sum_jexp(x_j)}\\
& =softmax(x_i)
\end{aligned}
$$
即,如果输入各维减去同一个数,softmax结果不变。
于是,可以令$l \rightarrow l-l_{k+1} $, $l_{k+1}=0$,$p=softmax(l)$保持不变。
期望号略去不写,利用$exp(l_{k+1})=1$,后两种代价变为:
$$
L_u = - \ln[1-p(k+1|x)] = -\ln[\frac{\sum_{j=1}^k\exp l_j}{\sum_{j=1}^k\exp l_j + \exp l_{k+1}}] \\
= -ln\sum_{j=1}^k\exp l_j + \ln(1+\sum_{j=1}^k\exp l_j )
$$
上述推导可以让我们省去k+1,让分类器仍然输出K维的估计l。
对于第一个代价,由于分类器输入必定来自前K类,所以可以直接使用l的前K维:
$$L_{l}=-\ln\left[ p(y|x,y<k+1)\right]=-\ln \left[\frac{\exp l_y}{\sum_{j=1}^k \exp l_j}\right]=-l_y + \ln\left[ \sum_{j=1}^k \exp l_j\right]$$
引入两个函数,使得书写更为简洁:
$$
LSE(x) = \ln[\sum_{j=1}\exp(x_j)]
$$$$
softplus(x) = \ln(1+\exp(x))
$$
三个误差:
$$
L_l = -l_y + LSE(l)
$$
$$
L_u = -LSE(l) + softplus(LSE(l))
$$
$$
L_f = softplus(LSE(l))
$$
优化目标
对于分类器来说,希望上述误差尽量小。引入权重w,得到分类器优化目标:
$$
L_D = L_l + \frac{w}{2}(L_u + L_f)
$$
对于生成器来说,希望其输出的伪样本能够骗过分类器。生成器优化目标与分类器的第三项相反:
$$
L_G = -L_f
$$
实验
本文的实验包含三个图像分类问题。分类器接受图像x,输出K类分类结果l。生成器从均匀分布的噪声z生成一张图像x。
MNIST
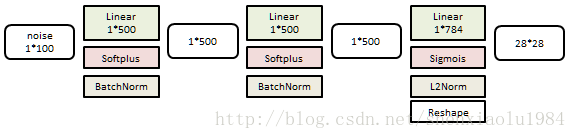
10分类问题,图像为28*28灰度。
生成器是一个3层线性网络:
分类器是一个6层线性网络:
训练样本60K个,测试样本10K个。
选择不同数量的训练样本给予标记,考察测试样本中错误个数。使用不同随机数种子重复10次:
| 有标记样本 | 20 | 50 | 100 | 200 |
|---|---|---|---|---|
| 占比 | 0.033% | 0.083% | 0.17% | 0.33% |
| 错误个数 | 1677±452 | 221±136 | 93±6.5 | 90±4.2 |
Cifar10
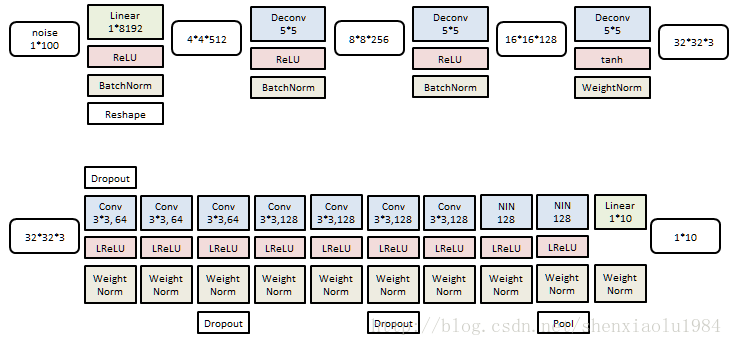
10分类问题,图像为32*32彩色。
生成器是一个4层反卷积网络:
分类器是一个9层卷积网络:
训练样本50K个,测试样本10K个。
选择不同数量的训练样本给予标记,考察测试样本中错误个数。使用不同的测试/训练分割重复10次:
| 有标记样本 | 1000 | 2000 | 4000 | 8000 |
|---|---|---|---|---|
| 占比 | 2% | 4% | 8% | 16% |
| 错误个数 | 21.83±2.01 | 19.61±2.09 | 18.63±2.32 | 17.72±1.82 |
SVHN
10分类问题,图像为32*32彩色。
生成器(上)以及分类器(下)和CIFAR10的结构非常类似。
训练样本73K,测试样本26K。
选择不同数量的训练样本给予标记,考察测试样本中错误个数。使用不同的测试/训练分割重复10次:
| 有标记样本 | 500 | 1000 | 2000 |
|---|---|---|---|
| 占比 | 0.68% | 1.4% | 2.7% |
| 错误个数 | 18.84±4.8 | 8.11±1.3 | 6.16±0.58 |
Reference:
- Salimans, Tim, et al. “Improved techniques for training gans.” Advances in Neural Information Processing Systems. 2016.
- https://arxiv.org/pdf/1406.2661.pdf
- https://blog.csdn.net/shenxiaolu1984/article/details/75736407
- https://blog.csdn.net/szm21c11u68n04vdclmj/article/details/78420955
- https://blog.csdn.net/xierhacker/article/details/75216652